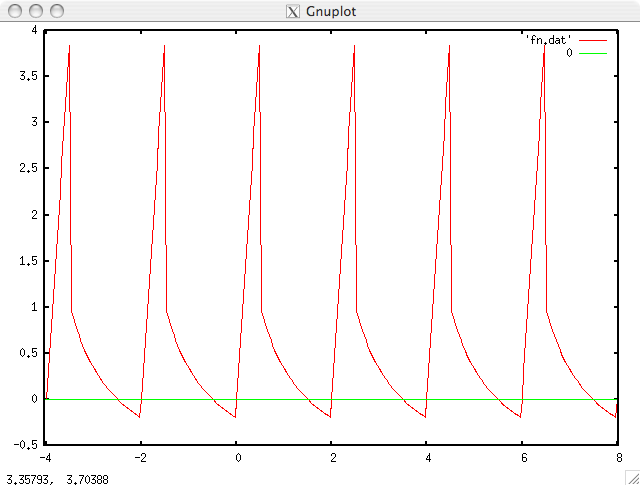

The program writes a file commands.gplot of GNUPLOT instructions
plot 'fn.dat' w lines, 0
This will tell GNUPLOT to plot the points listed in the file called fn.dat and to connect them
"with lines" and to plot the function y = 0, the horizontal axis.
Then the display is to show until the window is overclicked by mouse.
You can call up GNUPLOT and enter the same instructions at the gnuplot> prompt.
Then the program writes a datafile fn.dat which consists of x and y
coordinates along the graph of the function in sequence. We show the first few and last few lines:
pause mouse
-4.000000000000000 0.000000000000000
-3.960000000000000 0.320000000000000
-3.920000000000000 0.640000000000001
-3.880000000000000 0.960000000000001
...
7.920000000000000 -0.173553719008264
7.960000000000001 -0.186991869918699
8.000000000000000 0.000000000000000
The files are closed. During the execution of the program, the system directive is issued
system("gnuplot commands.gplot");
This tells the program to stop at that point, and issue the system command (UNIX command in this case)
gnuplot commands.gplot
which directs GNUPLOT to execute the commands in the file commands.gplot.
Upon mouse click, terminating GNUPLOT, the program execution resumes at that point.
/******************************************************************************************************
Treibergs 4-13-6
Gnuplot Driver 1
Program to write data files and execution files that run the plotting software gnuplot from a C
program. Thanks to Prof. G. Gustafson for showing me how to do this.
drivegnuplo.c
******************************************************************************************************/
# include <stdio.h>
# include <stdlib.h>
# include <math.h>
double /* Function prototype. */
perfun ( double x, double p );
int
main( void )
{
double a, b, c, d, p, x;
int i;
FILE *fp; /* Declaration of file variable */
printf ( "Periodic Function Via Recursive Function Calls\n" );
printf ( " Enter period : " );
scanf ( "%lf", &p );
printf ( " Enter two endpoint values : " );
scanf ( "%lf %lf", &a, &b );
if ( b < a)
{ /* Swap a and b if b < a. */
c = a;
a = b;
b = c;
}
d = ( b - a ) / 300.0;
fp = fopen ( "commands.gplot", "w" ); /* Open commands file */
/* fopen returns a pointer to the file. */
/* "w" for writing files, "r" for reading. */
fprintf ( fp, "plot [ %f : %f ] \'fn.dat\' w lines, 0 \n", a - d, b + d );
fprintf ( fp, "pause mouse \n" );
fclose ( fp ); /* closing returns file to system. */
/* Newly written data may be lost without closing the file */
printf ( "\nFunction values from %f to %f are being printed to file \"fn.dat\"\n", a, b );
fp = fopen ( "fn.dat", "w" ); /* Open data file. */
for ( i = 0; i <= 300 ; i++ )
{
x = a + i * d;
fprintf ( fp, "%25.15f %25.15f\n", x, perfun ( x, p ) );
}
fclose( fp );
system("gnuplot commands.gplot");
return EXIT_SUCCESS;
}
/* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
double
perfun ( double x, double p )
{
/* perfun grows linearly from 0 to p/4, then droops. */
double result;
if ( x < 0.0 )
result = perfun ( x + p, p );
else if ( x >= p )
result = perfun ( x - p, p );
else
{
if( x <= 0.25*p)
result = 16.0 * x / p;
else
result = 1.0 / ( 0.25 + x / p ) - 1.0;
}
return result;
}
/**************************************************************************************************
Treibergs April 14, 2006
Segment and Circle Plotter
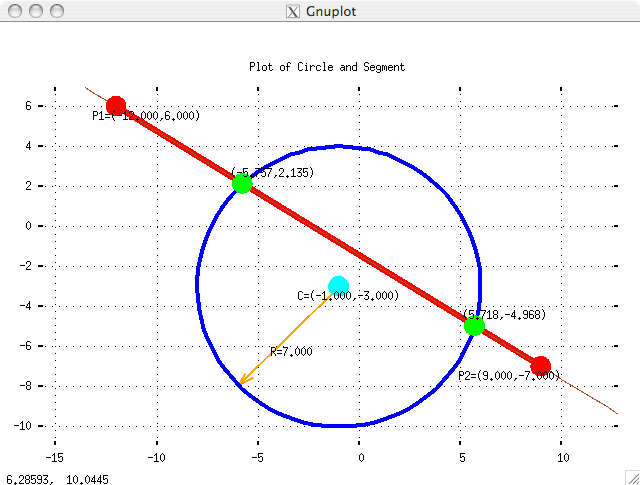
We use our third solution to problem 6b, to compute the intersection points, if any, of the given
segment and circle. Then we output a file gnufoo.gplot of GNUPLOT instructions.
For example, a typical run provides the following instructions in this file
reset
unset border
set grid nopolar
unset key
set style line 2 lt 7 lw 2
set arrow 1 from -7.000000,8.000000 to 6.000000,-5.000000 nofilled linetype 1 linewidth 6.000 size first 0.100,40.000,90.000
set style arrow 2 head nofilled size screen 0.03,15 ls 2
set arrow from -1.000000, 3.000000 to -5.949000,-1.949000 as 2
set parametric
set size ratio .625 1,1
set label 1 "P1=(-7.000,8.000)" at -5.560000,7.520000 centre norotate front nopoint
set label 2 "P2=(6.000,-5.000)" at 4.560000,-5.480000 centre norotate front nopoint
set label 3 "C=(-1.000,3.000)" at -0.520000,2.520000 centre norotate front nopoint
set label 4 "(-6.424,7.424)" at -4.984429, 7.904429 centre norotate front nopoint
set label 5 "(3.424,-2.424)" at 4.864429, -1.944429 centre norotate front nopoint
set label 6 "R=7.000" at -3.320000, -0.280000 centre norotate front nopoint
set title "Plot of Circle and Segment" 0.000000,0.000000 font ""
set xrange [ -14.440000 : 12.440000 ] noreverse nowriteback
set yrange [ -5.900000 : 10.900000 ] noreverse nowriteback
plot [t=-pi:pi] -1.000000+7.000000*sin(t), 3.000000 + 7.000000*cos(t) with lines lw 4 lt 3,
-0.500000+ (-6.500000)*t ,1.500000+(6.500000)*t with lines 6,
-7.000000+0.480000*sin(t) , 8.000000 +0.480000*cos(t) with filledcurve 1 ,
6.000000 +0.480000*sin(t) , -5.000000 +0.480000*cos(t) with filledcurve 1 ,
-6.424429 +0.480000*sin(t), 7.424429 +0.480000*cos(t) with filledcurve 2,
3.424429+ 0.480000*sin(t),-2.424429+0.480000*cos(t) with filledcurve 2,
-1.000000+0.480000*sin(t), 3.000000+0.480000*cos(t) with filledcurve 5
pause mouse
Which tell GNUPLOT to draw the line segment (a blue arrow without heads),
an arrow to indicate tthe radius of the circle,
label the endpoints of the segment
label the center point
label the intersection points
write a title line
set the size of the output box
plot the blue circle
plot the brown extended line
plot red dots (filled circles) at the ends of the segment
plot green dots at the intersection points
plot a cyan dot at the center of the circle
then pause until mouseclick.
Finally, command the system to run GNUPLOT using instructions from our output file.
cirsegplo.c
******************************************************************************************************************/
# include <stdio.h>
# include <stdlib.h>
# include <math.h>
# include <string.h>
# define TOL (0.5e-7)
typedef struct /* Structure consists of two doubles */
{ /* Every type "point" has two vars called .x and .y */
double x;
double y;
} point;
typedef struct /* Represents a circle with center and radius */
{
point center;
double radius;
} circle;
typedef struct /* Nested structures: */
{ /* consists of two "point" structures */
point p1;
point p2;
} segment;
double
lengthsq( point v);
void
printv( point t);
void
printmn( int i, int m );
point
linco( point v, double cv, point w, double cw );
int
main( void )
{
FILE *fp; /* Declaration of file variable */
double r,r1,rho1,rho2,rho3,a,b,c,d,w1,w2,t1,t2,tz,t, xmin, xmax, ymin, ymax, dx, dy, rmax, rd;
int n=0;
point middle, first, second;
segment seg;
circle cir;
printf ( "Circle and Segment \n\n"
"For this program, a segment is INSIDE if none of its points have a\n"
"distance to the center greater than the radius. A segment is OUTSIDE\n"
"if none of its points have a distance to the center less than the radius.\n"
"Thus inside or outside segments may touch the circle at a point.\n\n" );
printf ( "Enter the center of the circle x y : " );
scanf ( "%lf%lf", &cir.center.x, &cir.center.y );
printf ( "Enter the radius of the circle r :");
scanf("%lf",&cir.radius);
r = cir.radius*cir.radius;
printf ( "Enter the segment's starting point x y : " );
scanf ( "%lf%lf", &seg.p1.x, &seg.p1.y );
printf ( "Enter the segment's ending point x y : " );
scanf ( "%lf%lf", &seg.p2.x, &seg.p2.y );
if ( fabs(seg.p1.x - seg.p2.x)+fabs(seg.p1.y-seg.p2.y) < TOL ) /* degenerate case p1=p2 */
{
r1 = lengthsq(linco(seg.p1,1.0,cir.center,-1.0))-r;
if ( fabs(r1)< TOL)
{
printv( seg.p1);
printmn(1,1);
n = 1;
first=seg.p1;
}
else if (r1>0)
{
printmn(2,0);
n =0;
}
else
{
printmn(0,0);
n =0;
}
}
else
{
middle = linco ( seg.p1, 0.5, seg.p2, 0.5);
rho1 = lengthsq ( linco (seg.p1, 1.0, cir.center,-1.0) );
rho2 = lengthsq ( linco (seg.p2, 1.0, cir.center,-1.0) );
rho3 = lengthsq ( linco (middle, 1.0, cir.center,-1.0) );
a = (rho1+rho2)/2.0 - rho3;
b = (rho2-rho1)/2.0;
c = rho3-r;
d = b*b-4.0*a*c;
tz = -0.5*b/a;
if( fabs(d) < TOL) /* case extended line along segment is tangent to the circle */
{
if ( fabs(tz)<1.0+ TOL )
{
first = linco ( seg.p2,(1.0+tz)/2.0,seg.p1,(1.0- tz)/2.0);
printv ( first );
printmn(2,1);
n = 1;
}
else
{
printmn(2,0);
n = 0;
}
}
else if( d< 0.0) /* case extended line segment is outside the circle */
{
printmn(2,0);
n = 0;
}
else /* case extended segment passes through the circle */
{
t = sqrt(d)/(2.0*a);
t1 = tz-t; /* quadratic formula for zeros of quadratic */
t2 = tz+t;
n=0; /*n counts number of zeros (intersections with circle) in segment */
if( fabs(t1)<1.0+ TOL ) /* if first root is in segment */
{
n=1;
first = linco ( seg.p2,(1.0+t1)/2.0,seg.p1,(1.0- t1)/2.0);
printv( first );
}
if( fabs(t2) < 1.0+TOL ) /* if second root is in segment */
{
second = linco ( seg.p2, (1.0+t2)/2.0, seg.p1, (1.0- t2)/2.0 );
printv( second );
n = n + 1;
if ( n == 1 )
first = second;
}
if( (t1>1.0-TOL) && ( t2 >1.0-TOL) ) /* if both roots are on positive side of segment */
printmn(2,n);
else if( (t1< TOL - 1.0) && ( t2 < TOL - 1.0 ) ) /* else if both on neg side */
printmn(2,n);
else if( ( fabs(t1)> 1.0-TOL ) && (fabs(t2) > 1.0-TOL) ) /* else if one on each side */
printmn(0,n);
else /* remaining casi is that one of the roots is an interior point of segment */
printmn(3,n);
}
}
/* Start the plotting.
First compute the size of the bounding box using the dimensions of the circle and segment. */
xmin = cir.center.x - cir.radius;
xmax = cir.center.x + cir.radius;
ymin = cir.center.y - cir.radius;
ymax = cir.center.y + cir.radius;
if( xmin > seg.p1.x )
xmin = seg.p1.x;
if( xmin > seg.p2.x )
xmin = seg.p2.x;
if( ymin > seg.p1.y )
ymin = seg.p1.y;
if( ymin > seg.p2.y )
ymin = seg.p2.y;
if( xmax < seg.p1.x )
xmax = seg.p1.x;
if( xmax < seg.p2.x )
xmax = seg.p2.x;
if( ymax < seg.p1.y )
ymax = seg.p1.y;
if( ymax < seg.p2.y )
ymax = seg.p2.y;
dx = xmax - xmin;
dy = ymax - ymin;
rmax = dx;
if( 1.6 * dy > rmax)
rmax = 1.6 * dy;
rd = 0.02*rmax;
/* Then write the file with plotting instructions based on the computations and inputs. */
fp = fopen ( "gnufoo.gplot", "w" ); /* Open commands file */
fprintf( fp, "reset\n");
fprintf( fp, "unset border\n");
fprintf( fp, "set grid nopolar\n");
fprintf( fp, "unset key\n");
fprintf( fp, "set style line 2 lt 7 lw 2\n");
fprintf( fp, "set arrow 1 from %f,%f to %f,%f nofilled linetype 1 "
" linewidth 6.000 size first 0.100,40.000,90.000\n",seg.p1.x,seg.p1.y,seg.p2.x,seg.p2.y);
fprintf( fp, "set style arrow 2 head nofilled size screen 0.03,15 ls 2\n");
fprintf( fp, "set arrow from %f, %f to %f,%f as 2\n",cir.center.x,cir.center.y,cir.center.x-0.707*cir.radius,cir.center.y-0.707*cir.radius);
fprintf( fp, "set parametric\n");
fprintf( fp, "set size ratio .625 1,1\n");
fprintf( fp, "set label 1 \"P1=(%.3f,%.3f)\" at %f,%f centre norotate front nopoint\n",seg.p1.x,seg.p1.y,seg.p1.x+3*rd,seg.p1.y-rd );
fprintf( fp, "set label 2 \"P2=(%.3f,%.3f)\" at %f,%f centre norotate front nopoint\n",seg.p2.x,seg.p2.y,seg.p2.x-3*rd,seg.p2.y-rd );
fprintf( fp, "set label 3 \"C=(%.3f,%.3f)\" at %f,%f centre norotate front nopoint\n",cir.center.x,cir.center.y,cir.center.x+rd,cir.center.y-rd);
if( n >= 1)
fprintf( fp, "set label 4 \"(%.3f,%.3f)\" at %f, %f centre norotate front nopoint\n",first.x,first.y,first.x+3*rd,first.y+rd);
if( n>= 2)
fprintf( fp, "set label 5 \"(%.3f,%.3f)\" at %f, %f centre norotate front nopoint\n",second.x,second.y,second.x+3*rd,second.y+rd);
fprintf( fp, "set label 6 \"R=%.3f\" at %f, %f centre norotate front nopoint\n", cir.radius,cir.center.x-0.4*cir.radius+rd,cir.center.y-0.4*cir.radius-rd);
fprintf( fp, "set title \"Plot of Circle and Segment\" 0.000000,0.000000 font \"\"\n");
fprintf( fp, "set xrange [ %f : %f ] noreverse nowriteback\n", 0.5*(xmin+xmax)- 0.56*rmax, 0.5*(xmin+xmax)+ .56*rmax );
fprintf( fp, "set yrange [ %f : %f ] noreverse nowriteback\n", 0.5*(ymin+ymax)- .35*rmax, 0.5*(ymin+ymax)+ .35*rmax );
fprintf( fp, "plot [t=-pi:pi] %f+%f*sin(t), %f + %f*cos(t) with lines lw 4 lt 3, ", cir.center.x,cir.radius ,cir.center.y,cir.radius );
fprintf( fp, " %f+ (%f)*t ,%f+(%f)*t with lines 6, "
, 0.5*(seg.p1.x+seg.p2.x), 0.5*(seg.p1.x-seg.p2.x), 0.5*(seg.p1.y+seg.p2.y), 0.5*(seg.p1.y-seg.p2.y) );
fprintf( fp, " %f+%f*sin(t) , %f +%f*cos(t) with filledcurve 1 , ",seg.p1.x,rd,seg.p1.y,rd);
fprintf( fp, " %f +%f*sin(t) , %f +%f*cos(t) with filledcurve 1 , ",seg.p2.x,rd,seg.p2.y,rd);
if( n>= 1)
fprintf( fp, " %f +%f*sin(t), %f +%f*cos(t) with filledcurve 2,", first.x,rd,first.y,rd);
if( n >= 2)
fprintf( fp, " %f+ %f*sin(t),%f+%f*cos(t) with filledcurve 2,", second.x,rd, second.y,rd);
fprintf( fp, " %f+%f*sin(t), %f+%f*cos(t) with filledcurve 5\n",cir.center.x, rd, cir.center.y , rd);
fprintf( fp, "pause mouse\n");
fclose( fp ); /* File must be closed for system to be able to access it. */
/* Then issue the system command to execute GNUPLOT using the instructions from the written file. */
system( "gnuplot gnufoo.gplot");
return EXIT_SUCCESS;
}
/* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
/* Example of a double valued function that takes a "struct coords' argument. */
double
lengthsq( point v)
{
return v.x * v.x + v.y * v.y ;
}
/* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
point
linco ( point v, double cv, point w, double cw )
{
point temp;
temp.x = cv * v.x + cw * w.x;
temp.y = cv * v.y + cw * w.y;
return temp;
}
/* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
void
printv( point t)
{
printf(" A point of the intersection is ( %f, %f )\n",t.x,t.y);
return;
}
/* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */
void
printmn( int i, int m )
{
static char *mess[4]={"inside", "on","outside","neither inside nor outside"};
printf(" The segment is %s the circle.\n"
" The number of intersection points is %d \n\n", mess[i], m);
return;
}