Fernando Guevara Vasquez's homepage
Home Research Teaching
Math 5750/6880 Optimization (Fall 2008)
Class information
Class meets: MWF 9:40am - 10:30am
Where: LCB 225
Textbook: J. Nocedal and S. Wright, Numerical Optimization, Springer, second edition.
Prerequisites: Linear algebra (Math 2270 or similar), vector calculus (Math 2210 or similar) and basic Matlab knowledge. Permission from the instructor.
Contact information
Instructor: Fernando Guevara Vasquez
Office: LCB 212
Office hours: MWF 11am-12pm or by appointment
Phone number: +1 801-581-7467
Email: fguevara(AT)math.utah.edu
(replace (AT) by @)
Syllabus
The syllabus is available here: syllabus.pdfGrading
Homeworks 40%, Final project 60%
Homeworks will be given roughly biweekly. The project will consist on applying the methods we see in class to your particular research problem or to a problem chosen in conjunction with the instructor.
Announcements ![[RSS]](../images/rss14x14.png)
(Sat, Dec 27, 2008, 08:16 AM)
Your grades for Math 5750 and 6880 have been submitted to the registrar. You should have received an email with your class grade, HW grade, project grade and presentation grade. Taking both classes together the average grade is a B+, and here is a histogram (with the two classes together):
| A | ######## |
| A- | ### |
| B+ | ## |
| B | # |
| B- | |
| C+ | ## |
| C | |
| C- | # |
| D+ | |
| D | |
| D- | |
| E | # |
(Tue, Dec 9, 2008, 04:51 PM)
Some comments on the Project Reports:
- The official due date is Friday 12/12. However I will not grade them until Friday 12/19, so you have until 12/19 turn them in, on the condition that after 12/12 all reports should be submitted by email to the instructor. If you do not receive a confirmation email within 24h of your submission, please resend your report.
- If submitting your report by email you can still write it by hand to save time. Ask Paula in the Math department office to show you how to use the scanner (only B&W scanner is available).
- What I am expecting to see is about 5 pages (or more) on what is the problem you solved, what methods you used to solve it and a comparison of the different methods that summarizes the numerical experiments you ran.
- After I am done grading the projects I will send you back an annotated PDF or an email with my observations and your grade for the project and the class.
(Mon, Dec 1, 2008, 09:13 PM)
Thanks to Hilary for spotting the following typos (corrected in the newest versions of project.pdf and eit.tgz):
- File
fobj_GNHessian.m, line 44 should be:H = J'*kron(eye(nb),pars.Qbdry)*J; - Fixed typos in Section 5 of project.pdf. In the description of the Gauss-Newton Hessian approximation computation (3) should be
 and (4):
and (4):  .
.
(Mon, Dec 1, 2008, 03:21 PM)
- Today we started derivative free optimization methods. Lecture notes are available here: opti020.pdf (see also Chapter 9 in N&W).
- Here are the Project presentation schedules. It is not necessary to bring your laptop for the presentations. Just bring your slides in a USB key or email them to me before class. Tou can also present with the slide projector or even on the board. The order of the talks below is not fixed.
- F 12/5: Seth (translation), Joey (radio tomography)
- M 12/8: Joshua (tumor treatment with heat), Tao (transportation), Hong (EIT)
- W 12/10: Jaggadeesh (semantic indexing), Jiarong (EIT), Hilary (EIT), Eric (financial), Andy (calibration)
- F 12/12: Shawn (optimal structure), Mingxing (EIT), Carlos (EIT), Qin (EIT), Scott (vascularization), Ge (EIT)
(Wed, Nov 26, 2008, 01:42 PM)
Today we continued with trust region method (including for SQP). Lecture notes are here: opti019.pdf.
(Mon, Nov 24, 2008, 09:10 PM)
- The project presentations will be held on F 12/5, M 12/8, W 12/10 and F 12/12. Please email me if you have a preference, otherwise I will assign a day to you. You can present with slides, projector or even on the chalkboard.
- Common project: 5 min presentation. Describe your numerical experiments with the project problem and present your results.
- Other projects: 10 min presentation.
- Common project tips:
- The gradient is easier to check if you set
pars.V=eye(nbe);(or data for some conductivity) instead of the suggestedrandn(nbe). - To check that the adjoint state method is correctly implemented (independently of the regularization terms) you can set
pars.alpha=0. Regularization is needed to solve for the minimization, so do not leavepars.alphaas such.
- The gradient is easier to check if you set
(Fri, Nov 21, 2008, 04:37 PM)
- Today we finished the discussion on reduced SQP methods. We started trust region methods, here are the lecture notes for today and Monday: opti018.pdf.
- Fixed a typo in the project instructions project.pdf. The computation of the residual in section 4 ((b) in page 5) should be
 (Thanks to Hilary for spotting this).
(Thanks to Hilary for spotting this).
(Wed, Nov 19, 2008, 02:55 PM)
- Lecture notes for Wednesday are here: opti017.pdf, we covered reduced SQP methods.
- A clarification on HW4: The convention for the sign of the Lagrange multipliers in the provided EQP solver is the one used throughout the book, namely:
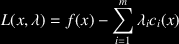 . Your SQP algorithm should be consistent with this convention in order for it to converge.
. Your SQP algorithm should be consistent with this convention in order for it to converge.
(Fri, Nov 14, 2008, 03:20 PM)
Homework 4 is due Monday December 1st 2008 and is here: hw4.pdf. Supporting code is:
- eqp.m An equality constrained quadratic programming solver using the nullspace approach
- test_eqp.m tests the above code on a the simple Example 16.2 of the textbook.
- f_18_3.m The objective function in Problem 18.3 in the textbook.
(Fri, Nov 14, 2008, 09:30 AM)
The common project support files and instructions have been updated: project.pdf and eit.tgz. A demo will be given tomorrow.
(Thu, Nov 13, 2008, 10:11 AM)
- Lecture notes for Monday and Wednesday are available here: opti016.pdf, we saw SQP methods and the L1 merit function.
- On Friday’s lecture I do a demo on how the common project should work.
(Wed, Nov 5, 2008, 09:20 PM)
The lecture notes for today and Monday are here: opti015.pdf. We covered interior point methods for quadratic programming and bound constrained optimization.
(Fri, Oct 31, 2008, 06:55 PM)
- Homework 3 is due Friday November 14 and is here: hw3.pdf.
- The simplex method implementation mentioned in HW3 is here: simplex.m.
- Lecture notes for Quadratic Programming are available here: opti014.pdf.
(Fri, Oct 24, 2008, 02:30 PM)
Today we continued the discussion on the simplex method and today we started interior point methods for linear problems. The class notes are here: opti013.pdf. The next homework will be available next week, you will have to implement your own interior point solver and use it to solve l1 minimization problems.
(Tue, Oct 21, 2008, 11:42 PM)
If you submit your Matlab code listings electronically I prefer if you send them as a single PS or PDF file. Here is how to do it (and this helps you if you want to print the code with syntax hightlighting):
- using the unix command
a2ps
a2ps -o outfile.ps -2 -A virtual -g -Ematlab4 file1.m file2.m file3.m
- using the Latex package
listings, create a document containing essentially the following. (you could add headers to indicate which file you are listing etc…)
\documentclass{article} \usepackage{listings} \begin{document} \lstset{language=Matlab,basicstyle=\small,breaklines=true} \lstinputlisting{file1.m} \lstinputlisting{file2.m} \lstinputlisting{file3.m} % etc ... \end{document}
(Mon, Oct 20, 2008, 10:56 PM)
- Today we reviewed Linear Programming and its dual problem. We set the stage for the Simplex method. Lecture notes are here: opti012.pdf.
- About the project:
- common project: you do not need to submit a proposal since what you have to do is already well defined. Though do start working seriously on it now. You will not have enough time to complete the project if you start during the last two weeks of classes.
- project from your research: you may submit the final proposal up to next week (Fri Oct 31). (Same advice as above: start working on it now)
(Fri, Oct 10, 2008, 01:32 PM)
- Lecture notes for today and last Wednesday are available here: opti011.pdf. We saw the dual linear problem today.
- The office hours during the break are cancelled. I’ll be out of town but joinable by email though.
- For HW2:
- If you need extra time or you are concerned about not been able to come ask questions during the break, you can turn your homework in by Wednesday October 22.
- Expressing the Tikhonov solution with the SVD (i.e. in terms of the singular values, vectors,
band the regularization parameter α) may not be easy if you are not familiar with the SVD, so this will be an extra credit part. However, you still have to find an expression for the solution.
- Common project: Here is some code to get you started with EIT: eit.tgz (to untar this in a unix system:
tar zxvf eit.tgz). A companion PDF file that explains the code and shows how to compute gradients using the adjoint state method is here as well: project.pdf.
(Mon, Oct 6, 2008, 05:12 PM)
- HW2 clarification on Problem 3. For the truncated SVD the solution to the linear least squares problem to give is the minimal norm solution (we saw how to obtain this for the full SVD in class, see opti006.pdf)
- Today we saw how considering part of the KKT conditions as a system of non-linear equations, the invertibility of its Jacobian is linked to the first and second order optimality conditions for constrained optimization. Lecture notes for today are here: opti010.pdf.
(Fri, Oct 3, 2008, 05:51 PM)
Today we continued with constrained optimization, we saw the first and second order optimality conditions. We will get back to this next time. The class notes are here: opti009.pdf.
(Thu, Oct 2, 2008, 08:28 PM)
- On Wed lecture we started constrained optimization theory (Chapter 12). Lecture notes will be posted later.
- A couple of precisions about HW2 (thanks to Joey for spotting these)
- In heat_demo.m, line 20 should be
plot(xtrue)and notplot(x)(already updated in the website) - Here is the file heat.m that generates an inverse heat equation problem. It comes from the Regularization Tools for Matlab of Per Christian Hansen (in the Sofware.zip file). This contains many regularization techniques and methods to choose regularization paramters. Please see the documentation, if you want to know more about these techniques.
- In heat_demo.m, line 20 should be
(Mon, Sep 29, 2008, 04:48 PM)
- Today’s lecture was a crash course on the finite element method, this is still part of explaining the common project.
- HW2 is due Monday October 20 (after the fall break). Please don’t leave for the last moment as it requires some experimenting.
- Problem 1 [Finite difference approximation] Do a log-log plot of the error of approximation error of the derivative of
exp(x)atx=1, using forward finite differences and centered differences forh= 10.^(0:-1:-20). Explain your results. Are the empirical optimal values forhand the errors in the approximations of the order predicted by the theory, assuming the only error is floating point error (ε = O(10-16))? Note: for forward differences h* = O(ε1/2); for centered difference h* = O(ε1/3). The error for forward differences is O(ε1/2) and for centered differences O(ε2/3). - Problem 2 [Curve fitting, non-linear least squares] Please dowload the chapter on least-squares of Numerical Computing with MATLAB by Cleve Moler. Reproduce the data fitting example presented in section 5.8 (p 17) using your BFGS implementation from HW1. However, do solve for all four parameters β1, β2, λ1, λ2, instead of finding βi in terms of λi as is presented in the text. This involves writing a function
[f,g] = expfit(x,pars), wherexis a vector containing the four unknown parameters, and figure out what is the gradient.
Update:- The struct
parshelps this time: you can use it to give your function the data pointsyandt. - Experiment different initial guesses for the parameters and include plots for a good and not so good fit. Avoid negative parameters.
- The struct
- Problem 3 [Linear least squares] The two following regulariaztion methods can be used to solve the linear least squares problem outlined in heat_demo.m (with
bnoisy).- Truncated SVD: Solving the linear least squares problem with Ak (the approximation of A obtained by keeping only the singular vectors/values corresponding to the k largest singular values) instead of A.
- Tikhonov regularization: Minimizing 0.5*norm(A*x – bnoisy)2 + alpha*norm(x)2 instead of 0.5*norm(A*x-bnoisy)2, where norm is the 2-norm.
Both methods involve the choice of a regularization parameter (k for TSVD, or alpha for Tikhonov). - Derive explicit solutions to TSVD and Tikhonov using the SVD of A. If you found this somewhere else, please cite it.
- Study the images obtained with different values of these parameters. Report cases that you deem interesting and the ``best’’ values for
alphaandk. - Use the SVD to explain why the error obtained by solving the unregularized problem can get so large.
- Problem 1 [Finite difference approximation] Do a log-log plot of the error of approximation error of the derivative of
(Fri, Sep 26, 2008, 12:10 PM)
- Notes for the Mon, Wed and Fri lectures are here: opti008.pdf.
- This week was dedicated to the computation of derivatives. We saw finite differences approximation of the gradient and Hessian, handy identities with the Fréchet derivative and the adjoint state method which when it can be applied can considerably save computations. I include the derivation of the gradient for the continuum problem. Do not panic if you do not understand this, you need only to understand what happens in the discrete case for the project.
- The adjoint state method was illustrated with Electrical Impedance Tomography (EIT).
- A good reference for the adjoint state method is the book “Computational Inverse Problems” by Curtis Vogel (SIAM Frontiers in Applied Mathematics).
- A good review of the EIT problem and its applications is: Cheney, Isaacson, Newell, Electrical Impedance Tomography, SIAM Review 41, 1, pp. 85-101, DOI: http://dx.doi.org/10.1137/S0036144598333613.
- Project Information: You have two options for your project,
- Common project: Solve the EIT problem. I will provide all the discretization code, you will have to piece things together to compute the derivatives using the adjoint method (this procedure will be clearly outlined), and then use the Gauss-Newton method to image the conductivity using your choice of regularization functional. A preliminary version of the sample code will be shown in class.
- Your own research: Choose a problem related to your research/work or of your interest that preferably fits in the framework we presented in class (continuum differentiable problems). Some other guidelines:
- Depending on the complexity of your problem, you do not need to solve an optimization problem. For example calculating the derivatives using the adjoint state method or even formulating the problem could be enough. These alternatives should only be chosen in conjunction with the instructor.
- You do not need to do anything new, e.g. you can replicate results from a paper.
- Project Deadlines:
- Mon October 8 — Preliminary project proposal: you have to choose the problem to solve and communicate your choice to the instructor before this deadline. There is no write up due, but if you are planning on doing a project on your own research, I strongly recommend that you come to my office to help you find a good problem (even if you have come already).
- Mon October 22 — Final project proposal: you should have the problem to solve reasonably well formulated, and a plan of how to solve it. A short write up is due (1-2 pages should be enough).
- Fri Dec 5 – Fri Dec 12 — Project presentations (10-15 min, possibly less if doing the common project)
- Fri Dec 12 — Project reports due (hand written is OK)
(Fri, Sep 19, 2008, 11:06 AM)
On Wednesday’s lecture we resumed the discussion on Linear Least squares problems. Today’s lecture was on Non Linear Equations (Chapter 11). Notes are available here: opti007.pdf.
(Thu, Sep 18, 2008, 01:48 PM)
HW1: Here are more clarifications
- If you need extra time to do HW1 you may turn it in on Monday Sep 22. I am not going to grade anything before then. However I plan to assign a new homework tomorrow.
- The steepest descent algorithm can take several thousand iterations to converge. So make sure the maximum number of iterations
opts.maxitis large enough or reduce the toleranceopts.tol. - For the gradient and Hessian check functions:
- Pick
xandvas you like (providedxis not a stationary point andvis a nonzero vector) - Don’t be alarmed if for e.g. the gradient check, the first order residual does not appear quadratic for big
t(Taylor theorem does not hold) or too smallt(floating point error kicks in). We will study this better next week.
- Pick
(Tue, Sep 16, 2008, 03:53 PM)
In Monday’s lecture we got started with non-linear least squares (chapter 10). Notes are available here: opti006.pdf.
(Fri, Sep 12, 2008, 12:30 PM)
- Today we saw inexact Newton’s method and in particular Newton-CG. We got started with Non-Linear Least Squares. The notes are here: opti005.pdf.
- HW1: Here are answers for several questions I’ve had about the homework.
- Problem 3.9: please do not implement Algorithm 3.5 for finding the step size using the strong Wolfe conditions, it can take longer than I thought to write. Instead use backtracking, always checking that skTyk > 0 (for this particular example convergence can be attained in a few iterations). If this does not happen, keep the same approximation to the inverse Hessian for the next iteration.
- Whenever you need backtracking, use Armijo (Algorithm 2.1 with rho=1/2). Also the initial step size for all the algorithms we’ve seen so far is 1.
- A good value for the constant c1 in the sufficient decrease condition is
1e-4.
(Thu, Sep 11, 2008, 03:16 PM)
The file steepest_descent.m I handed out has a typo on line 31, where the maximum number of iterations was set to 100 even if you had set opts.maxit to something else. The file linked above corrects the problem, or change line 31 to:
if ~isfield(opts,'maxit') opts.maxit=100; end; % default max iterations
Let me know if you spot any other bugs like this one.
(Wed, Sep 10, 2008, 08:44 PM)
We saw the theory behind the conjugate gradient (CG) method (Chap 5). Next time we will briefly go back to CG to address preconditioning and Newton-CG methods (p 165-170). Then we will start least-squares problems (Chap 10).
(Mon, Sep 8, 2008, 03:09 PM)
We reviewed BFGS and DFP, practical considerations and convergence theory. We got started with the linear conjugate gradient method (Chap 5). The notes are here: opti004.pdf, but most of this material will be covered next Wednesday.
(Fri, Sep 5, 2008, 12:14 PM)
- Today we finished convergence of line search methods and we got started with Quasi-Newton methods (Chap 6). Notes for today: opti003.pdf.
- HW1 due Fri Sept 19 2008
- Do problems 2.1, 2.2, 3.1, 3.9. You may use these Matlab functions (Octave compatible) as a model.
- quad.m defines a quadratic function (minimizer x* = (0,0)T)
- steepest_descent.m does steepest descent (in a broken way where the step size is fixed).
Example usage of these functions (works with octave as well)
Here the function to optimize is passed in the form of a “function handle”opts.tol=1e-5; % set tolerance to stop computations [f,g] = steepest_descent([1;1],@quad,[],opts)
@quad(perhaps@rosenbrockin your code). If the function you want to optimize needs extra data, you can pass it in the structurepars(which in this case is just an empty struct[]).
- Write functions
check_gradient(f,x,v,pars)andcheck_hessian(f,x,v,pars)that check that the gradient and Hessian information returned by the functionfevaluated atxis consistent with Taylor’s theorem in directionv.
Hint: For the gradient test you can check that the residual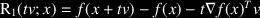 behaves like t2 for say t = 10-k, k = 0,…,10 (in Matlab
behaves like t2 for say t = 10-k, k = 0,…,10 (in Matlab t=10.^[0:-1:-10]).
Use these functions to check your gradient and Hessian computations for the Rosenbrock function.
- Do problems 2.1, 2.2, 3.1, 3.9. You may use these Matlab functions (Octave compatible) as a model.
(Wed, Sep 3, 2008, 11:34 AM)
We covered line search methods (pp30-41 in N&W). Plan for next time: convergence results for line-search methods. Quasi-Newton methods. Lecture notes for today are here: opti002.pdf.
(Tue, Sep 2, 2008, 11:06 PM)
- On lecture 3 (Fri Aug 29) we proved local convergence of Newton’s method (see also p44). Next time: we will see how to obtain global convergence.
- The Math Department’s Computer lab is located between LCB and JWB in the T. Benny Rushing Mathematics Center, room 155C. Matlab may also be available on other campus computer labs.
- The only reason you will need your math computer lab account in this class is for using Matlab. So if you have acces to Matlab by other means (e.g. in other computer labs on campus, your personal copy etc…) or you want to use another software (Octave, etc…), you don’t need to set up this account.
(Wed, Aug 27, 2008, 05:01 PM)
- We covered some preliminaries (see A.1) and necessary and sufficient optimality conditions (2.1: pp 11-17).
- All registered students to this class have an account in the computer lab. To login please follow these instructions. Please do make sure you can login as the first assignement will be given next week and it will involve some Matlab programming. Contact me if you have problems with your initial login.
- Matlab is not required but it is recommended, as sample code will be given in this language. You can also use Octave which is an open source alternative to Matlab, but I do not guarantee that the sample code I give will be octave compatible.
- Please check your UMail email, if you have not received an email from the class by tomorrow, contact me. Announcements will be available here and through the class mailing list (your UMail ‘unid@utah.edu’ email account was added automatically when you registered). If you do not use this account that often I recommend you forward your UMail with the uNID Account Tools
(Tue, Aug 26, 2008, 10:36 PM)
In lecture 1 we reviewed optimization for functions of the real line. Notes for this lecture are available here: opti001.pdf.