Limit of an infinitely fast wiggling curve

Next: Hidden length! Up: ``Strange'' limits Previous: Distributions and weak limits:

Limit of an infinitely fast wiggling curve

The limiting infinitely fast wiggling curve

$\begin{displaymath}{\cal G}= \lim \sin( \omega x),\quad \omega \rightarrow \infty \end{displaymath}$

is not a function either: Although the range of its values is

, one cannot compute its value ${\cal G}(x)$ for any specific

except

$\begin{figure} \Huge {Animated figure to be inserted here} \end{figure}$

In addition, its average over any interval is zero, and its weak limit (see the discussion of the term in 4.3.2) is zero:

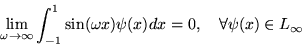$\begin{displaymath} \lim_{\omega \rightarrow \infty} \int_{-1}^1 \sin( \omega x) \psi(x) dx =0, \quad \forall \psi(x)\in L_\infty \end{displaymath}$

(2)

However, some moments of ${\cal G}$ are nonzero. The second moment is:

$\begin{displaymath}\lim_{\omega \rightarrow \infty} \int_{-1}^1 \sin^2( \omega x... ...ver 2} + {1 \over 2} \cos(2 \omega x) \right) dx ={1 \over 2} \end{displaymath}$

Similarly, higher even moments are non-zero:

$\begin{eqnarray*} \lim_{\omega \rightarrow \infty} \int_{-1}^1 \sin^3( \omega x... ...rrow \infty} \int_{-1}^1 \sin^4( \omega x) dx & =& {3 \over 8} \end{eqnarray*}$

and so on.

Andre Cherkaev
2001-11-16