Finite Elements

The key ingredient of finite elements is that the interpolant is determined uniquely on each triangle by data on that triangle. There are two ways widely used to make this possible:

• Choosing a sufficiently large polynomial degree
• Subdividing the triangle.

We illustrate both techniques.

Quintic Elements

This element is quintic on each triangle. The coefficients at the points marked with red stars are obtained by interpolating to function values and partial derivatives to second order at each vertex. The points marked green are obtained either by interpolating to a perpendicular cross boundary derivative at the midpoint of edge edge, or by the requirement that perpendicular cross-boundary derivatives (CBDs) be cubic along each edge.

The result is a scheme that's piecewise quintic, globally C ¹, and that reproduces quintic (if one interpolates to CBDS) or quartic (if one enforces a cubic CBD) polynomials exactly.

An interpolant constructed like this on every triangle of a triangulation will lie in a subspace of S with r=1 and d=5.. It will only be a subspace since the interpolant is twice differentiable at every vertex of the triangulation.

The Clough-Tocher Element

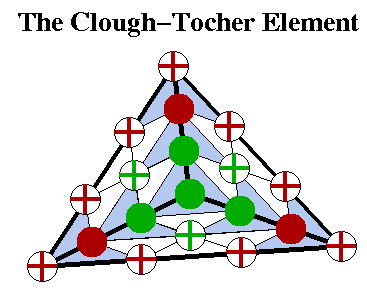
This element is obtained by dividing each triangle in the triangulation about its centroid into three subtriangles called microtriangles. On each micro triangle the interpolant is cubic.

The Figure nearby shows an ordinary minimal determining set. Coefficients at the three red points at each vertex of the macrotriangle are obtained by interpolating to function values and gradients at the vertices of the triangle. The green points in the minimal determining set are obtained similarly as in the quintic element, either by interpolating to perpendicular CBDs at the centers of the edges, or by requiring that the perpendicular CBDs be linear along each edge.

The result is a schemed that's piecewise cubic, it requires only function and first order derivative values, and it reproduces quadratic or linear functions exactly.

A double Clough-Tocher C ² Element

I gained my first serious experience with the Bernstein-B ézier form when I designed this element (see item 22 on my Bibliography. ) Click on the small image to see a larger and clearer version.

The macrotriangle is split about its centroid into three subtriangles each of which is again split about its centroid, called a subcentroid, into three subtriangles, for a total of 9 microtriangles. The scheme is piecewise quintic and internally and globally twice differentiable. It is significant in the design of the scheme that the triples of vertex-centroid-subcentroid are colinear.

The development in the original paper is different, but it can be described in the terms of a minimal determining set as follows:

1. Pick the green points to interpolate to function values and derivatives through second order at the vertices of the macrotriangle.
2. Pick the red points to enforce global smoothness, by making the first order perpendicular CBD cubic along each edge of the macro triangle and the second CBD Derivative linear.
3. Pick the blue points such that the interpolant is quartic along each edge from a vertex to the centroid.
4. Pick the cyan points to make the interpolant cubic along each edge from the centroid to a subcentroid.
5. Finally, pick the coefficient at the magenta point in the minimal determining set (i.e., the centroid), such that the sum of tangential fourth order derivatives on the lines from the vertices to the centroid equals zero.

The result is a globally twice differentiable interpolation scheme that requires only data of the same order as the degree of smoothness, and that reproduces cubic polynomials exactly.

[15-Mar-1999]