

Parabolas
The Graph of  .
.

Figure 1. A parabola
The
graph of an equation involving  and
and  is the set of all
points
is the set of all
points  in the
cartesian coordinate plane
whose coordinates satisfy the equation.
The
graph of a function
in the
cartesian coordinate plane
whose coordinates satisfy the equation.
The
graph of a function  is the graph of the equation
is the graph of the equation
 For example, Figure 1 shows the graph of the equation
For example, Figure 1 shows the graph of the equation
This particular graph is an example of a parabola. Note that it
is symmetric with respect to the  -axis which is called its axis or line
of symmetry. The lowest point on the parabola (which in this case is the origin)
is called its vertex.
-axis which is called its axis or line
of symmetry. The lowest point on the parabola (which in this case is the origin)
is called its vertex.
We'll use this graph and equation to illustrate some
ideas that have much wider applicability. Let's consider making some
changes:
Rescaling
Suppose we multiply the value of  with a constant. Let's call it
with a constant. Let's call it
 .
Thus we obtain the new equation
.
Thus we obtain the new equation
If  this is the same equation as before. Let's consider some other
possibilities, however:
this is the same equation as before. Let's consider some other
possibilities, however:

Figure 2. Several parabolas
Figure 2 shows the graphs of these equations for
Graphs can be similarly reflected, stretched or compressed in the
horizontal direction by multiplying  with a constant. However,
in the present simple example this effect is equivalent to a
vertical rescaling since
with a constant. However,
in the present simple example this effect is equivalent to a
vertical rescaling since
 where
where  .
.
Translations
Consider now the effect of subtracting a constant  from
from  :
:
This is equivalent to
and so it has the effect of
raising the graph of  by
by  units. Of course, if
units. Of course, if  is
negative, the graph is lowered (by
is
negative, the graph is lowered (by  units).
units).
Subtracting a constant  from
from  has the same effect in the
horizontal direction. Consider the equation
has the same effect in the
horizontal direction. Consider the equation
and
compare it with the original equation  . As in
. As in  ,
,  is never negative. It assumes its minimum value (
is never negative. It assumes its minimum value ( ) at
) at  .
Thus the graph of
.
Thus the graph of  is that of
is that of  shifted
shifted  units to
the right. If
units to
the right. If  is negative, the graph is shifted
is negative, the graph is shifted  units to
the left.
units to
the left.
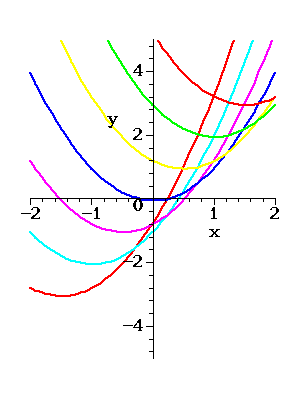
Figure 3. Translated Parabolas
Horizontal and vertical shifts can be combined, and any such
combination is called a translation. The general form of a
translation applied to  is given by
is given by
which is
often written as
A translation does not change the
shape or orientation of a graph. It only changes its
location. Figure 3 shows translations of the graph of  with
with
The Completed Square Form
The completed square form of a quadratic function  is
is
Its graph is a parabola whose vertex is  .
If
.
If  it opens up, if
it opens up, if  it opens down. (If
it opens down. (If  the
graph is a horizontal line which you can think of a s a degenerate
parabola.) The vertical line
the
graph is a horizontal line which you can think of a s a degenerate
parabola.) The vertical line  is the axis or line of
symmetry of the parabola.
is the axis or line of
symmetry of the parabola.
It is clear how a general quadratic polynomial
can be converted to the standard form. Just complete the square, as
illustrated in the following example:
The graph of this particular equation is given in Figure 4.
The resulting parabola has  and the vertex (
and the vertex ( . It is
obtained from the standard parabola
. It is
obtained from the standard parabola  by reflecting it thorough
the
by reflecting it thorough
the  -axis, stretching it vertically and translating it 1 unit to
the left and 8 units up. Note that all of these properties can be
immediately
read off the equation
-axis, stretching it vertically and translating it 1 unit to
the left and 8 units up. Note that all of these properties can be
immediately
read off the equation

Figure 4. Another Parabola
Scaling and Translating Graphs
The principles illustrated here apply to any equation, so let's
restate them:
- A combination of horizontal and vertical shifts is a
translation of the graph, a combination of horizontal and
vertical compression and stretching is a scaling of the
graph.
- Adding a constant
 to
to  shifts the graph
shifts the graph  units
to the right if
units
to the right if  is positive, and to the left if
is positive, and to the left if  is
negative.
is
negative.
- Adding a constant
 to
to  shifts the graph
shifts the graph  units up
if
units up
if  is positive, and down if
is positive, and down if  is negative.
is negative.
- Multiplying
 with a positive constant
with a positive constant  compresses the
graph horizontally if
compresses the
graph horizontally if  and stretches it horizontally if
and stretches it horizontally if  .
If
.
If  is negative these effects are combined with a reflection
through the
is negative these effects are combined with a reflection
through the  axis.
axis.
- Multiplying
 with a positive constant
with a positive constant  compresses the
graph vertically if
compresses the
graph vertically if  and stretches it vertically if
and stretches it vertically if  .
If
.
If  is negative these effects are combined with a reflection
through the
is negative these effects are combined with a reflection
through the  axis.
axis.
As usual, I recommend that you do not memorize these facts. Rather
think about what's happening in terms of the interplay between the
graph and the equation, and figure out the effect of what you are
doing, or what you need to do, rather than relying on remembering
arcane facts.



![]() and
and ![]() is the set of all
points
is the set of all
points ![]() in the
cartesian coordinate plane
whose coordinates satisfy the equation.
The
graph of a function
in the
cartesian coordinate plane
whose coordinates satisfy the equation.
The
graph of a function ![]() is the graph of the equation
is the graph of the equation
![]() For example, Figure 1 shows the graph of the equation
For example, Figure 1 shows the graph of the equation
![]() with a constant. Let's call it
with a constant. Let's call it
![]() .
Thus we obtain the new equation
.
Thus we obtain the new equation


![]() with a constant. However,
in the present simple example this effect is equivalent to a
vertical rescaling since
with a constant. However,
in the present simple example this effect is equivalent to a
vertical rescaling since
![]() where
where ![]() .
.
![]() is given by
is given by