|
|
Last update(s):
Tue Oct 18 15:11:19 2005
Tue Nov 15 18:46:42 2005
Fri Oct 6 15:01:23 2006
Wed Feb 24 14:40:47 2010
Wed May 2 18:40:40 2012
Wed Jun 29 09:07:24 2022
![]()
MAXIMA is a reimplementation in Common Lisp of MACSYMA, the oldest computer algebra system. MAXIMA provides both symbolic computation and high-precision integer and floating-point arithmetic.
MACSYMA was originally developed starting about 1968 at the Massachusetts Institute of Technology, using the MACLISP dialect of the Lisp programming language. The name stood for Project MAC's SYmbolic MAnipulation System, and MAC stands for Man and Computer, or for Machine Aided Cognition. Project MAC later became the MIT Laboratory for Computer Science, certainly one of the premier institutions in the field.
In the early 1980s, Macsyma was reimplemented in the Franz Lisp dialect by Richard Fateman's research group at the University of California at Berkeley, enabling it to be run on DEC VAX computers running Berkeley UNIX, where it was called Vaxima. It was also ported by a U.S. Department of Energy-supported effort at MIT, to NIL, another Lisp dialect. The U.S. DOE version was further developed by William Schelter at the University of Texas in Austin under the name Maxima, until his untimely death in July 2001. Maxima has since been released under the GNU General Public License and has its own Web site.
What books are available for MAXIMA?
More than two dozen. See the macsyma bibliography.
What documentation is available online for MAXIMA?
The MAXIMA manual is available in the Emacs info system, also accessible via the standalone xinfo utility.
There is a brief introduction to MAXIMA in the local file /usr/local/src/maxima/intromax.pdf and a more detailed user manual in the local file /usr/local/src/maxima/maxima.pdf.
There is also a help system inside MAXIMA. In a MAXIMA session, invoke the describe() function:
% maxima
...
(C1) describe(sqrt)
0: ISQRT :(maxima.info)Definitions for Operators.
1: SQRT :Definitions for Operators.
2: SQRTDISPFLAG :Definitions for Operators.
Enter n, all, none, or multiple choices eg 1 3 : 1
Info from file /export/local/share/info/maxima.info:
- Function: SQRT (X)
the square root of X. It is represented internally by X^(1/2).
Also see ROOTSCONTRACT. RADEXPAND[TRUE] - if TRUE will cause nth
roots of factors of a product which are powers of n to be pulled
outside of the radical, e.g. SQRT(16*X^2) will become 4*X only if
RADEXPAND is TRUE.
(D1) FALSE
What version of MAXIMA do we have?
Most of our systems have just a single version of MAXIMA. You can see what is available like this:
% which maxima /usr/local/bin/maxima % ls /usr/local/bin/maxima-* ls: No match. % maxima -version Maxima 5.9.0pre-cvs (with enhancements by W. Schelter). ...
How do I use high-precision arithmetic?
Assign the desired decimal precision to the fpprec variable, and then enter numerical expressions with exact arguments for evaluation as arguments of the bfloat() (big float) function, or with big-float numbers containing power-of-ten exponents in the form bnnn. Here is an example:
% maxima ... (C1) fpprec : 50$ (C2) bfloat(sin(-15/2)); (D2) - 9.3799997677473885794846379814904723643183139550804B-1 (C3) sin(-7.5b0); (D3) - 9.3799997677473885794846379814904723643183139550804B-1 (C4) sin(1b0/256) / (1/256); (D4) 9.9999745687042983799221222193087945750276128903456B-1 (C5) bfloat(sin(1/256) / (1/256)); (D5) 9.9999745687042983799221222193087945750276128903456B-1 (C6) 40!; (D6) 815915283247897734345611269596115894272000000000
You can convert the result of a symbolic expression to a numeric value in native hardware floating-point arithmetic with the numer option at the end of an expression:
% maxima
...
(%i1) sin(-15/2);
15
(%o1) -sin(--)
2
(%i2) sin(-15/2), numer;
(%o2) - .9379999767747389
(%i3) sqrt(17);
(%o3) sqrt(17)
(%i4) %, numer;
(%o4) 4.12310562561766
Be warned, however, that hardware precision is fixed at 53 bits, or roughly 16 decimal digits, and it may be inadequate.
How do I make a simple 2-D function plot?
MAXIMA has a pop-up GUI that can be used to display plots:
% maxima ... (C3) plot2d(sin(x)/x, [x, -5, 5], [y, -1, 1]);
The resulting plot looks something like this:
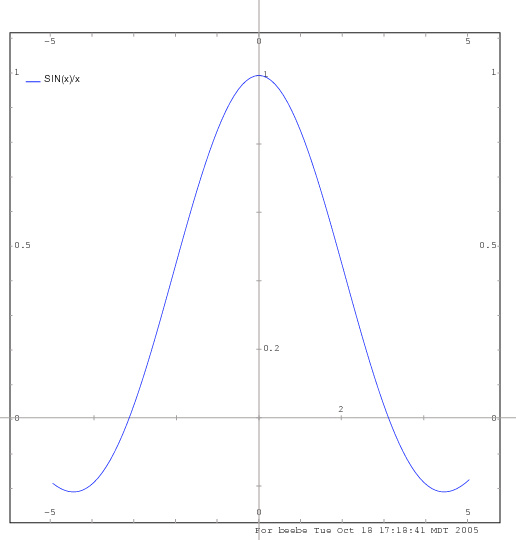
Move the cursor to the upper-left corner to get a popup menu that will allow you to save the plot as a PostScript file. The file is saved in your home directory under a fixed filename sdfplot.ps. Then select the Dismiss button in the pop-up to return control to the MAXIMA terminal session.
How do I make a 3-D surface plot?
MAXIMA has a pop-up GUI that can be used to display surface plots:
% maxima ... (C3) plot3d(sin(sqrt(x^2+y^2))/sqrt(x^2+y^2),[x,-12,12],[y,-12,12]);
The resulting plot has a red dot at the origin, and looks something like this:

You can grab a corner of the surrounding wireframe and manipulate the figure to get a desired view, then save it just like with the 2-D plot described in an earlier question on this Web page.
One such view, with the surface turned upside down, looks like this (the red origin dot is on the upper right):
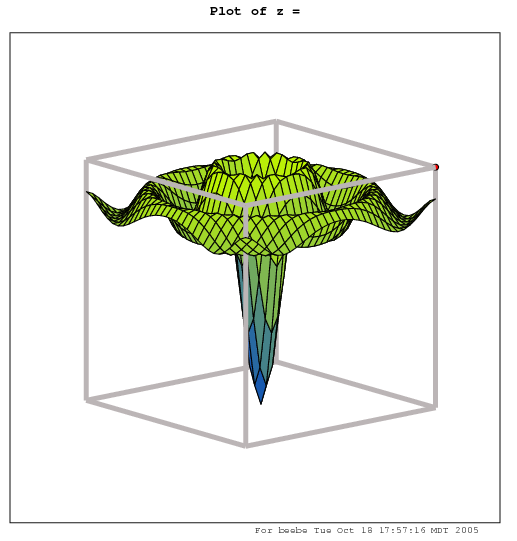
The MAXIMA info pages show how to produce more complex self-intersecting surfaces, like Möbius bands and Klein bottles.
I'm working on machine X. Why does it not have MAXIMA?
MAXIMA is a large and complex system. At version 5.27.0 [30-Apr-2012], the MAXIMA source code consists of about 380,000 lines of Common Lisp, 26,000 lines of Fortran, and 600 lines of C. MAXIMA can be compiled to interface to any of about a half-dozen different implementations of Common Lisp; on most of our systems, it uses CLisp (clisp), but on others, it uses GNU Common Lisp (gcl) or Steel Bank Common Lisp (sbcl). We attempt to build each new release of Maxima, and one or more Common Lisp systems, on all of our platforms, and by 2012, most systems have both Maxima and Common Lisp. However, no local build of MAXIMA has yet been successful for MirBSD and OpenBSD (both IA-32). All other systems have one or more versions installed. If you wish to obtain MAXIMA for use on a personal computer, please contact systems staff for help and advice: the software, and the assistance, are free.
How does Maxima compare with Maple and Mathematica?
While there is considerable subject overlap among symbolic algebra systems, there is little similarity in syntax, library functionality, or design philosophy, and we know of no automatic translation tools that can convert code from one symbolic-algebra language to another.
Nevertheless, if you are familiar with at least one of these languages, the Web page Maxima, Maple, and Mathematica: the Summary and its parent page The Playsome Threesome: Maxima, Maple, and Mathematica may be helpful. The first displays a large table of how to do common things in each of the three languages.
Is there a local mailing list for questions about MAXIMA?
No, there is not, but one can easily be created if there is sufficient user demand. In the meantime, students who use MAXIMA in courses should direct their questions to their instructors.