|
|
Last update:
Thu Oct 13 15:29:24 2005
...
Tue Jul 10 12:53:31 2012
![]()
Mathematica is a programming language and optional GUI environment for symbolic algebra and high-precision decimal integer and floating-point arithmetic. Its design began in the late 1980s, and has always been done as a commercial effort by the vendor, Wolfram Research, Inc.
Mathematica is licensed for use at selected University of Utah departments who share its cost. If you have a computer login account in one of the participating departments, then you already have access to Mathematica for use in classroom teaching and in research.
Under NO circumstances may the software be used for commercial or other nonacademic purposes.
The license is administered by systems staff members of the Mathematics Department. Contact them for further information about the availability of Mathematica for university personnel, and license requirements.
What books are available for Mathematica?
About 380 of them: see the extensive Mathematica bibliography.
What documentation is available locally online for Mathematica?
Relatively little, apart from the help system inside Mathematica. You can use it like this:
% math ... In[1]:= ?Sqrt Sqrt[z] gives the square root of z.
The vendor has numerous Web sites that may be helpful: they can all be found at links from the Wolfram Web Resources site.
Vendor online documentation can be located via their search facility.
There is a single PDF file stored at /usr/local/sys/mathematica/8.0.1/SystemFiles/IncludeFiles/TeX/texmf/doc/wolfram/msymdoc.pdf with the title The Mathematica Virtual Font Package: Mathematica Fonts for LaTeX2e.
There are also assorted HTML files scattered throughout the installation tree; you can search for them in the file /usr/local/sys/mathematica/FILES. None is of general interest to most users, and because they are under license, they cannot be made generally available via the Web. However, if you have login access to our facilities, you can view them as local disk files with your Web browser.
From mid-2008, the vendor offers a 15-minute screencast tutorial, A Hands-On Introduction to Mathematica It requires a workstation with audio support.
What version of Mathematica do we have?
The current version on Sun Solaris 10 SPARC is 7.0.1. Version 8.0.1 is available on GNU/Linux AMD64, IA-32, and IA-64, and Apple Mac OS X, systems.
The terminal version of Mathematica is named math, and the GUI version is named mathematica. Both are found in /usr/local/bin.
The mcc program is the MathLink template file compiler, for compiling C code that can be accessed from Mathematica.
How do I use high-precision arithmetic?
Use the N[expression,digits] function with the second argument set to the desired decimal precision, and the first argument the numerical expression to be evaluated. Here is an example:
% math
Mathematica 3.0 for Solaris
...
In[1]:= N[Erfc[-7.5`50], 50]
Out[1]= 1.9999999999999999999999999722335061396943089933603
In[2]:= N[Sin[1/256] / (1/256), 50]
Out[2]= 0.9999974568704298379922122219308794575027612890346
In[3]:= N[40!, 50]
47
Out[3]= 8.159152832478977343456112695961158942720000000000 10
WARNING: In Mathematica, all non-integral numeric constants must carry a precision suffix consisting of a backquote and the precision in decimal. This means that if you change the precision of your program, all numeric constants must be changed as well, even if they are exactly representable in decimal arithmetic. Omission of even one precision suffix can completely invalidate your numerical results!
Here is what happens if you fail to include the precision suffix:
In[7]:= N[Erfc[-7.5], 50] Out[7]= 2. In[8]:= N[Erfc[-15/2], 50] Out[8]= 1.9999999999999999999999999722335061396943089933603
How do I make a simple 2-D function plot?
In the GUI mode, Mathematica displays in the scrolling worksheet the results of a Plot[] function call.
% math
...
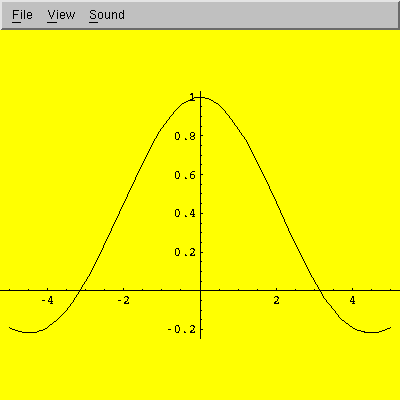
In[1]:= Plot[Sin[x]/x, {x, -5, 5}]
Out[1]= -Graphics-
The File -> Save As menu lets you save the graph in a special PostScript subset that Mathematica knows how to read. You can capture a snapshot of the pop-up window by running the X Window Dump command in a separate terminal window, piping its output into the ImageMagick format-conversion tool:
% xwd | convert - sin-x-over-x.png
xwd waits for you to move the pointer into the desired window and click the mouse to make the snapshot.
Another way to make the screen dump is to convert it to Portable Network Map (PNM) format, and then to PNG format:
% xwd | xwdtopnm | pnmtopng > sin-x-over-x.png
Here is what the plot-window snapshot looks like:
How do I make a 3-D surface plot?
Use the Plot3D[] function. Here is an example:
% math
...
In[1]:= Plot3D[Sin[Sqrt[x * x + y * y]] / Sqrt[x * x + y * y],
{x, -12, 12}, {y, -12, 12}]
Here is what a screen dump of the surface plot looks like (see the 2-D plotting question above for how to make such a dump):
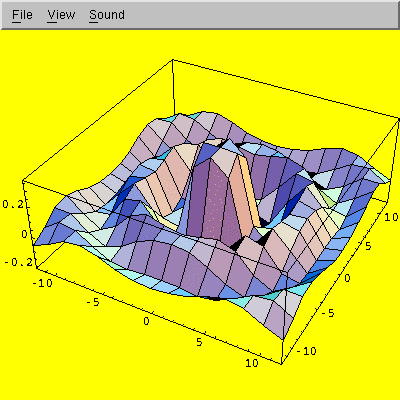
The View -> Rendering Options menu path in the pop-up window lets you toggle display of mesh lines and polygon filling.
The default mesh size is only 15×15, but you can easily increase it with the PlotPoints option:
In[2]:= Plot3D[Sin[Sqrt[x * x + y * y]] / Sqrt[x * x + y * y],
{x, -12, 12}, {y, -12, 12},
PlotPoints -> 51]
Here is what the new plot looks like:
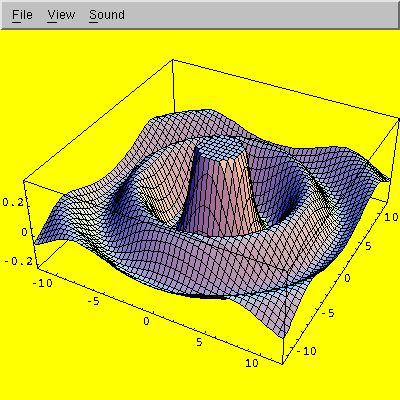
If you double-click on the graphics image, you can resize it. If you left-click on the image, you can rotate it in three dimensions. Right-click brings up a menu with further options.
You can use the ViewPoint option to select a different viewpoint:
In[3]:= Plot3D[Sin[Sqrt[x * x + y * y]] / Sqrt[x * x + y * y],
{x, -12, 12}, {y, -12, 12},
PlotPoints -> 51,
ViewPoint -> { 1, 1, 2 }]
That produces a plot like this:
![hat surface plot (large mesh, [1,1,2] viewpoint) in Mathematica](hat-high-112.png)
You can turn off the coloring with the Shading option:
In[4]:= Show[%, Shading -> False]
Here, we used the Show[] function to replot the last object, represented by the percent argument. The new plot looks like this:
![hat surface plot (large mesh, B/W, [1,1,2] viewpoint) in Mathematica](hat-high-bw.png)
More recent versions of Mathematica provide the Animate[] function to produce multi-frame animations.
How does Mathematica compare with Maxima and Maple?
While there is considerable subject overlap among symbolic algebra systems, there is little similarity in syntax, library functionality, or design philosophy, and we know of no automatic translation tools that can convert code from one symbolic-algebra language to another.
While Maxima and Maple are conventional procedural programming languages, Mathematica is primarily a functional programming language, in which most programming actions, other than simple assignments, are done by calls to functions, such as If[], While[], For[], Integrate[], D[] (differentiate), Sqrt[], and so on.
Nevertheless, if you are familiar with at least one of these languages, the Web page Maxima, Maple, and Mathematica: the Summary and its parent page The Playsome Threesome: Maxima, Maple, and Mathematica may be helpful. The first displays a large table of how to do common things in each of the three languages.
Is there a local mailing list for questions about Mathematica?
No, there is not, but one can easily be created if there is sufficient user demand. In the meantime, students who use Mathematica in courses should direct their questions to their instructors.